Bir eşkenar üçgen, üç tarafı da eşit uzunlukta olan bir üçgendir. Üçgen gibi iki boyutlu bir çokgenin yüzey alanı, çokgenin kenarlarının içerdiği toplam alandır. Bir eşkenar üçgenin üç açısı da Öklid geometrisinde aynı ölçüdedir. Öklid üçgeni açılarının toplam ölçüsü 180 derece olduğundan, bu, eşkenar üçgenin açılarının tümünün 60 derece olduğu anlamına gelir. Bir eşkenar üçgenin alanı, bir tarafının uzunluğu bilindiğinde hesaplanabilir.

Taban ve yükseklik bilindiğinde bir üçgenin alanını belirleyin. Taban s ve yüksekliği h olan her iki özdeş üçgeni atın. Bu iki üçgenle daima taban s ve yükseklik h paralelogramı oluşturabiliriz. Bir paralelkenarın alanı s x s olduğundan, bir üçgenin A alanı bu nedenle x s x s'dir.

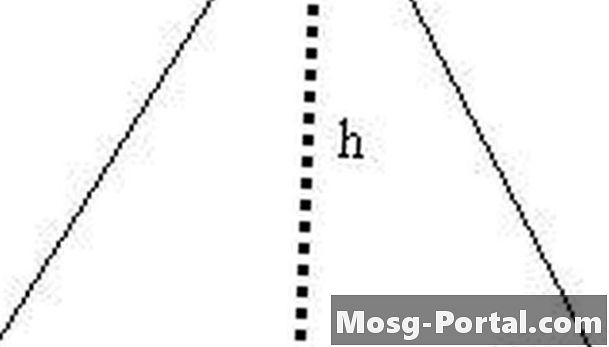
Eşkenar üçgeni, iki çizgi üçgeni şeklinde h çizgi parçasıyla oluşturun. Bu dik üçgenlerden birinin uzunluğu hipotenüsü, bacaklardan birinin h uzunluğu ve diğer bacağın uzunluğu s / 2'dir.
S'yi h cinsinden ifade eder. 2. adımda oluşturulan dik üçgeni kullanarak, Pisagor formülüyle s ^ 2 = (s / 2) ^ 2 + h ^ 2 olduğunu biliyoruz. Bu nedenle, h ^ 2 = s ^ 2 - (s / 2) ^ 2 = s ^ 2 - s ^ 2/4 = 3s ^ 2/4, ve biz şimdi h = (3 ^ 1/2) s / 2.
3. adımda elde edilen h değerini 1. adımda elde edilen üçgen alan formülü ile değiştirin. A = ½ sxh ve h = (3 ^ 1/2) s / 2 olduğundan, şimdi A = (s (3 ^ değerine sahibiz. 1/2) s / 2 = (3 ^ 1/2) (s ^ 2) / 4.
Kenarları 2 uzunluğunda olan bir eşkenar üçgenin alanını bulmak için 4. adımda elde edilen eşkenar üçgenin alanı için formülü kullanın. A = (3 ^ 1/2) (s ^ 2) / 4 = (3 ^ 1/2 ) (2 ^ 2) / 4 = (3 ^ 1/2).