İçerik
Sinüs kanunu ve kosinüs kanunu, bir üçgenin açılarının ölçülerini, yanlarının uzunluklarına bağlayan trigonometrik formüllerdir. Üçgenler içindeki daha büyük açıların zıt taraflarla orantılı olarak daha büyük olması özelliğinden türetilmiştir. Eğer bir taraf, bir açı ve bir ek taraf veya açı ölçüsü biliyorsanız, bir üçgenin kenarlarının uzunluğunu ve dörtgensel kenarların uzunluğunu hesaplamak için sinüs yasasını veya kosinüs yasasını kullanın.
Üçgen Yan Uzunluklarını Hesapla
Üçgenin değerlerini bulun. Veriler, yan uzunlukları ve zaten bilinen açı ölçüleridir.Bir açı, bir taraf ve başka bir taraf veya başka bir açının ölçüsünü bilmiyorsanız, üçgen kenar uzunluklarını bulamazsınız.
Üçgenin bir ASA, AAS, SAS veya ASS üçgeni olup olmadığını belirlemek için değerleri kullanın. Bir ASA üçgeni, iki açıyı birbirine bağlayan tarafın yanı sıra, iki açıya da sahiptir. Bir AAS üçgeni iki açıya ve boyut olarak farklı bir tarafa sahiptir. Bir SAS üçgeni iki tarafın oluşturduğu açının yanı sıra iki tarafa sahiptir. Bir ASS üçgeni iki tarafa ve açılara göre farklı bir açıya sahiptir.
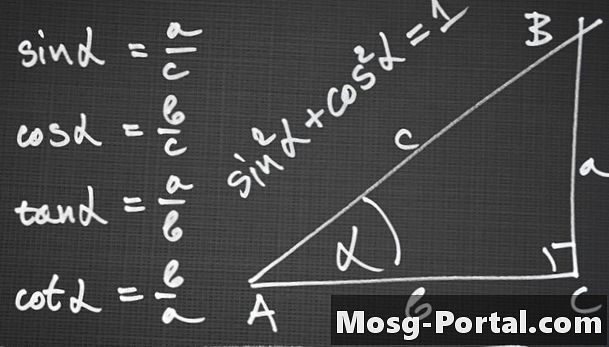
ASA, AAS veya ASS üçgeni ise, tarafların uzunluklarıyla ilgili bir denklem oluşturmak için sinüs yasasını kullanın. Sinüs yasası, üçgen açıları sinüslerinin oranlarının ve karşıt taraflarının eşit olduğunu belirtir: günah A / a = günah B / b = günah C / c, burada a, b ve c açıların zıt taraf uzunluklarıdır A, B ve C sırasıyla.
Örneğin, iki açının 40 derece ve 60 derece olduğunu ve bunlara katılan tarafın 3 birim uzunluğunda olduğunu biliyorsanız, günah 80/3 = günah 40 / b = günah 60 / c denklemini kurardınız (karşıt açıyı biliyorsunuz). 3 ünite uzunluğundaki taraf 80 derecedir, çünkü üçgen açıları toplamı 180 derecedir).
Bir SAS üçgeni ise, kenarların uzunluklarına ilişkin bir denklem oluşturmak için kosinüs yasasını kullanın. Kosinüslerin yasası, c ^ 2 = a ^ 2 + b ^ 2 - 2ab_cos C olduğunu belirtir. Başka bir deyişle, c tarafının uzunluğunun karesi, diğer iki taraf uzunluğunun kareleri eksi bu iki ürünün çarpımı kadardır. taraflar ve bilinmeyen tarafın karşısındaki açının kosinüsü. Örneğin, iki taraf 3 ünite ve 4 ünite olsaydı ve açı 60 derece olsaydı, c ^ 2 = 3 ^ 2 + 4 ^ 2 - 3_4 * cos 60 denklemini yazardınız.
Bilinmeyen üçgen uzunluklarını bulmak için denklemlerdeki değişkenleri çözün. B = 80/3 = sin 40 / b denkleminde b'nin çözülmesi b = 3 sin 40 / sin 80 değerini verir, bu nedenle b yaklaşık 2'dir. C = 80/3 = sin 60 / c denklemindeki c'nin çözülmesi c = 3 sin 60 / sin 80 değeri, c yaklaşık 2.6'dır. Benzer şekilde, c ^ c = 2 = 3 ^ 2 + 4 ^ 2 - 3_4_cos 60 denkleminde c'nin çözümü c ^ 2 = 25 - 6 veya c ^ 2 = 19 değerini verir, bu nedenle c yaklaşık 4.4'tür.
Quadrilateral Yan Uzunluklarını Hesapla
Dörtgen boyunca bir köşegen çizin (verilen herhangi bir açı ölçüsünü içermeyen köşegeni seçin; örneğin, eğer A açısı kuadrilateral ABCD'de verilen ise, B ve D köşegen bağlantısını çizin).
Bir ASA, SAS, AAS veya ASS üçgeni ayarlamak için göstergeleri kullanın. Dörtgenlerin açılarının toplamının 360 derece olduğunu unutmayın, böylece diğer üçünü biliyorsanız dördüncü açının ölçüsünü bulabilirsiniz.
Bir ASA, AAS veya ASS üçgeni kurarsanız, dört kenarlı tarafların uzunluklarını çözmek için sinüs yasasını kullanın. Bir SAS üçgeni ayarladıysanız, kenarların uzunluklarını çözmek için kosinüs yasasını kullanın.