İçerik
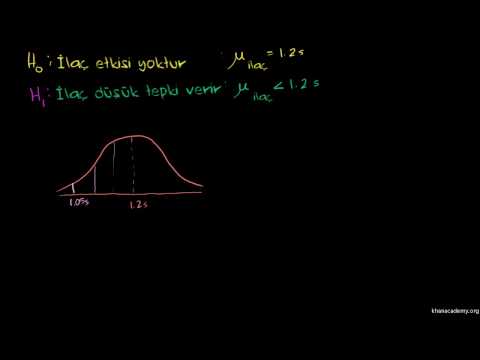
Çıkarımsal istatistiklerde, hipotezler araştırma sorularına geçici cevaplar olarak oluşturulmuştur. İstatistiksel hipotetik testler, örnek istatistiklere dayanarak popülasyon parametreleriyle ilgili hipotezleri değerlendirmemizi sağlar. Test tipi, ilgili değişkenlerin ölçüm seviyesine göre değişir. Bir popülasyon parametresinin bir değerden daha büyük veya daha küçük olduğu varsayılırsa, tek kuyruklu bir test kullanılır. Araştırma hipotezinde yön belirtilmediğinde, iki kuyruklu bir test kullanılır. İki kuyruklu bir test, ilgili değişkenlerin değerlerinde bir fark olup olmadığını gösterecektir.
Popülasyon parametreleri için veri toplayın. Parametreler için yöndeki belirli bir farkı belirten teorik bir temel olup olmadığını belirleyin. Belirtilen bir fark, bir değişkenin değerinin diğer değişkene göre daha yüksek veya daha düşük olduğunu belirterek belirtilecektir. Bu bilgi, iki kuyruklu bir testin uygun olup olmadığına karar vermenizi sağlar.
Değişkenin ölçüm seviyesi, örnekleme yöntemi, örneklem büyüklüğü ve popülasyon parametreleri ile ilgili varsayımlarda bulunun. Hipotezlerinizi formüle etmek için bu varsayımları kullanın. İlk hipoteziniz, araştırma hipoteziniz veya H1 olacaktır. Bu hipotez, popülasyon parametresinin değişkenlerindeki farkı belirtir. İkinci hipoteziniz, boş hipoteziniz veya H0 olacaktır. Bu hipotez, araştırma hipoteziyle çelişir ve popülasyon ortalaması ile belirli bir değer arasında bir fark olmadığını belirtir.
Alfa test istatistiklerini hesaplayın. Alfa, sıfır hipotezinin reddedilme olasılığının seviyesidir. Alfa geleneksel olarak 0,05, 0,0 veya 0,001 seviyelerine ayarlanır, bu da% 5,% 1 veya% 0,1 hata payı olacak demektir. İki kuyruklu bir test için, alfa değerini 2'ye bölün ve standart sapma biliniyorsa Z istatistiği ile veya standart sapma bilinmiyorsa t-istatistiği ile karşılaştırın.
Popülasyon parametresi arasında bir fark olup olmadığını belirlemek için boş hipotezi test edin. Amaç, araştırma hipotezine destek sağlamak için boş hipotezi reddetmektir. Olasılık değeri alfadan küçük olduğunda, sıfır hipotezini reddediyoruz ve araştırma hipotezini destekliyoruz. Olasılık değeri alfadan büyük olduğunda boş hipotezi reddedemeyiz.