İçerik
- Parabol
- Matematikçi Menaechmus
- "Parabol" Adı
- Galileo ve Mermi Hareketi
- Parabolik Reflektörler
- Asma köprüler
Parabol gibi matematiksel eğriler icat edilmedi. Aksine, keşfedildi, analiz edildi ve kullanıldı. Parabolün çeşitli matematiksel açıklamaları vardır, matematik ve fizikte uzun ve ilginç bir geçmişi vardır ve günümüzde birçok pratik uygulamada kullanılmaktadır.
Parabol
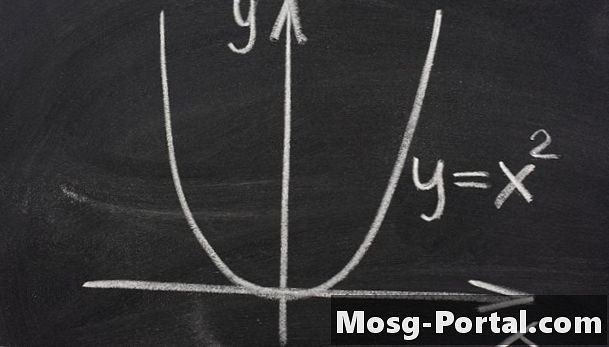
Bir parabol, kenarların sonsuz şekilde yükselmeye devam ettiği açık bir kaseye benzeyen sürekli bir eğridir. Bir parabolün matematiksel bir tanımlaması, odak denilen sabit bir nokta ve directrix denilen bir çizgiyle aynı mesafedeki noktaların kümesidir. Başka bir tanım parabolün belirli bir konik bölüm olmasıdır. Bu, bir koninin içinden geçip geçmediğinizi göreceğiniz bir eğri olduğu anlamına gelir. Koninin bir tarafına paralel dilimliyseniz, o zaman bir parabol görürsünüz. Bir parabol ayrıca, eğri y ekseni etrafında simetrik olduğunda, y = ax ^ 2 + bx + c denklemiyle tanımlanan eğridir. Diğer durumlar için daha genel bir denklem de vardır.
Matematikçi Menaechmus
Yunan matematikçi Menaechmus (orta dördüncü yüzyılda B.C.), parabolün konik bir bölüm olduğunu keşfetmesiyle alacaklıdır. Ayrıca, kuşağın iki kökü için geometrik bir yapı bulma problemini çözmek için parabolas kullanarak kredilendirildi. Menaechmus bu problemi bir inşaatla çözemedi, ancak çözümü iki parabolik eğri ile kesişerek bulabileceğinizi gösterdi.
"Parabol" Adı
Perga'nın Yunan matematikçi Apollonius'u (üçüncü ve ikinci yüzyıllar B.C.) parabolün isimlendirilmesiyle yatırılmaktadır. "Parabola", Çevrimiçi Etimoloji Sözlüğü'ne göre, "belirli bir alanın" uygulaması "tarafından verilen bir düz çizgiye uygulandığından" olduğu için, "kesin uygulama" anlamına gelen Yunanca bir kelimedir.
Galileo ve Mermi Hareketi
Galileo’nun zamanında, bedenlerin kareler kuralına göre düştüğü biliniyordu: Gidilen mesafe, zaman karesiyle orantılı. Ancak, mermi hareketinin genel yolunun matematiksel doğası bilinmiyordu. Topların gelişiyle bu önemli bir konu haline geldi. Galileo, yatay hareket ve dikey hareketin bağımsız olduğunu kabul ederek, mermilerin parabolik bir yol izlediğini gösterdi. Teorisi nihayetinde Newton’un çekim yasasının özel bir örneği olarak onaylandı.
Parabolik Reflektörler
Parabolik bir yansıtıcı, doğrudan kendisine gelen enerjiye odaklanma veya konsantre olma yeteneğine sahiptir. Uydu TV, radar, cep telefonu kuleleri ve ses toplayıcıların hepsi parabolik yansıtıcıların odaklanma özelliğini kullanır.Büyük radyo teleskopları, uzaktaki nesnelerin görüntülerini oluşturmak için uzaydan gelen soluk sinyalleri yoğunlaştırıyor ve günümüzde birçok büyük olanlar kullanılıyor. Yansıtan ışık teleskopları da bu prensip üzerinde çalışır. Maalesef, Arşimed’in bir Yunan ordusunun 213’te Syracuse kentine saldıran Roma gemilerini işgal etmek için ateş yakmak için parabolik aynaları kullanmasına yardım eden bir hikaye. Muhtemelen efsaneden fazla değildir. Odaklanma işlemi de tersten çalışır: Odaktan aynaya yayılan enerji çok düzgün bir düz huzmeye yansır. Radar ve mikrodalga gibi lambalar ve vericiler odaktaki bir kaynaktan yansıyan yönlendirilmiş enerji ışınlarını yayar.
Asma köprüler
Bir ipin iki ucunu tutarsanız, katener adı verilen bir eğri içine düşüyor. Bazı insanlar bu eğriyi bir parabol için yanlışlarlar, fakat gerçekte bir değildir. İlginçtir, ipten ağırlık asarsanız, eğri şekil değiştirir, böylece süspansiyon noktaları bir katener yerine bir parabolün üzerinde durur. Dolayısıyla asma köprülerin asılı kabloları aslında katener değil, parabol oluşturur.