
Otokorelasyon, zaman serileri analizi için kullanılan istatistiksel bir yöntemdir. Amaç, farklı zaman adımlarında ayarlanan aynı değerdeki iki değerin korelasyonunu ölçmektir. Zaman verileri hesaplanan otokorelasyonda kullanılmamasına rağmen, anlamlı sonuçlar alabilmek için zaman artışlarınızın eşit olması gerekir. Otokorelasyon katsayısı iki amaca hizmet eder. Bir veri kümesinde rastgele olmadığını tespit edebilir. Veri setindeki değerler rastgele değilse, o zaman otokorelasyon analistin uygun bir zaman serisi modelini seçmesine yardımcı olabilir.
Analiz ettiğiniz veriler için ortalamayı veya ortalamayı hesaplayın. Ortalama, veri değerlerinin sayısına bölünen tüm veri değerlerinin toplamıdır (n).
Hesaplamanız için zaman gecikmesine (k) karar verin. Gecikme değeri, kaç zaman adımının bir değeri diğerinden ayırdığını gösteren bir tamsayıdır. Örneğin, (y1, t1) ve (y6, t6) arasındaki gecikme beş'tir, çünkü iki değer arasında 6 - 1 = 5 zaman aşaması vardır. Rastgele olup olmadığını test ederken, diğer gecikme değerleri de çalışacak olsa da, genellikle gecikme k = 1 kullanarak yalnızca bir otomatik korelasyon katsayısı hesaplarsınız. Uygun bir zaman serisi modelini belirlerken, her biri için farklı bir gecikme değeri kullanarak bir dizi otokorelasyon değeri hesaplamanız gerekir.
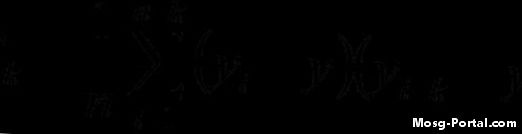
Verilen formülü kullanarak otokovaryans fonksiyonunu hesaplayın. Örneğin, üçüncü yinelemeyi (i = 3) bir k = 7 gecikmesi kullanarak mı hesaplıyordunuz, o zaman bu yinelemenin hesaplaması şöyle görünür: (y3 - y-bar) (y10 - y-bar) Tümüyle yineleyin "i" nin değerleri ve ardından toplamı alın ve veri kümesindeki değerlerin sayısına bölün.
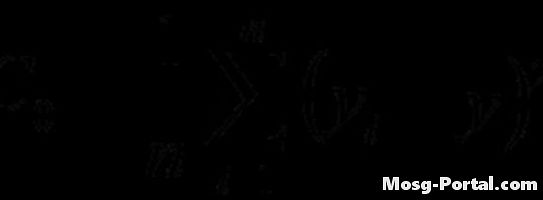
Verilen formülü kullanarak varyans fonksiyonunu hesaplayın. Hesaplama, otokovaryans fonksiyonuna benzer, ancak gecikme kullanılmaz.

Otokorelasyon katsayısını elde etmek için otokovaryans fonksiyonunu varyans fonksiyonuna bölün. Bu adımı, gösterildiği gibi iki işlev için formülleri bölerek atlayabilirsiniz, ancak çoğu zaman, kendi kendine kovaryansa ve varyansa başka amaçlar için ihtiyaç duyacaksınız, bu nedenle bunları ayrı ayrı hesaplamak pratiktir.