İçerik
Geometride, bir sekizgen sekiz tarafı olan bir çokgendir. Normal bir sekizgen, sekiz eşit yüzeye ve eşit açılara sahiptir. Normal sekizgen genellikle durma işaretlerinden tanınır. Bir oktahedron, sekiz taraflı bir polihedrondur. Normal bir oktahedronun kenarları eşit uzunlukta sekiz üçgen içerir. Etkili olarak üslerinde buluşan iki kare piramit var.
Sekizgen Alan Formülü
"A" uzunlukta kenarlara sahip normal bir sekizgen alanı için formül 2 (1 + sqrt (2)) a ^ 2'dir, burada "sqrt" kare kökü belirtir.
türetme
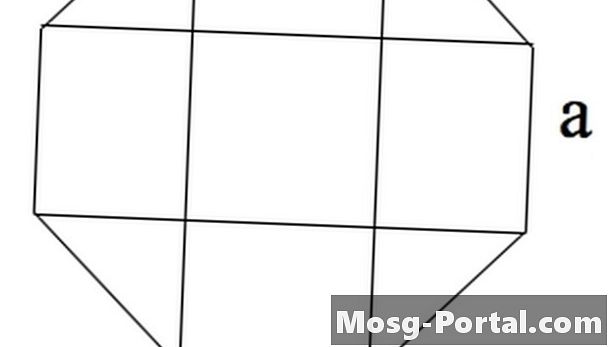
Bir sekizgen 4 dikdörtgen, merkezde bir kare ve köşelerde dört ikizkenar üçgen olarak görülebilir.
Kare a ^ 2 alanından oluşuyor.
Üçgenler Pisagor teoremi tarafından a, a / sqrt (2) ve a / sqrt (2) tarafına sahiptir. Bu nedenle, her biri ^ 2 / 4'lük bir alana sahiptir.
Dikdörtgenler a * a / sqrt (2) alanına sahiptir.
Bu 9 alanın toplamı 2a ^ 2 (1 + sqrt (2)).
Octahedron Hacim Formülü
"A" tarafındaki normal bir oktahedronun hacmi için formül bir ^ 3 * sqrt (2) / 3'tür.
türetme
Dört taraflı bir piramidin alanı taban alanı * 3 / 3'tür. Normal bir sekizgen alanı, bu nedenle 2x taban * yükseklik / 3'tür.
Temel = a ^ 2 önemsiz bir şekilde.
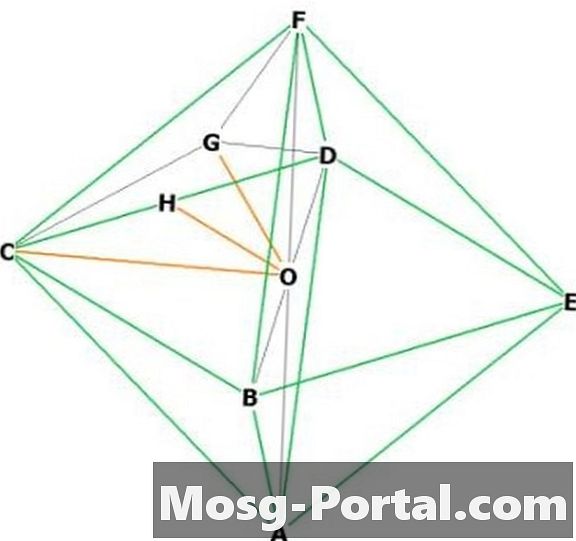
İki bitişik köşeyi seçin, "F" ve "C" deyin. "O" merkezinde. FOC, "a" tabanına sahip bir ikizkenar dik üçgendir, dolayısıyla OC ve OF, Pisagor teoremi tarafından a / sqrt (2) uzunluğundadır. Yani yükseklik = a / sqrt (2).
Böylece normal bir oktahedronun hacmi 2 * (a ^ 2) * a / sqrt (2) / 3 = a ^ 3 * sqrt (2) / 3 şeklindedir.
Yüzey alanı
Düzenli oktahedronların yüzeyi, "a" tarafının eşkenar üçgeninin 8 kez yüz alanıdır.
Pisagor teoremini kullanmak için, apeksten üsse bir çizgi bırakın. Bu, "a" uzunluğunun hipotenüsü ve bir yan uzunluğu "a / 2" olan iki sağ üçgen oluşturur. Bu nedenle, üçüncü taraf sqrt = sqrt (3) a / 2 olmalıdır. Böylece bir eşkenar üçgenin alanı yükseklik * taban / 2 = sqrt (3) a / 2 * a / 2 = sqrt (3) a ^ 2/4 şeklindedir.
8 kenarlı, normal bir oktahedronun yüzey alanı 2 x sqrt (3) * a ^ 2'dir.